
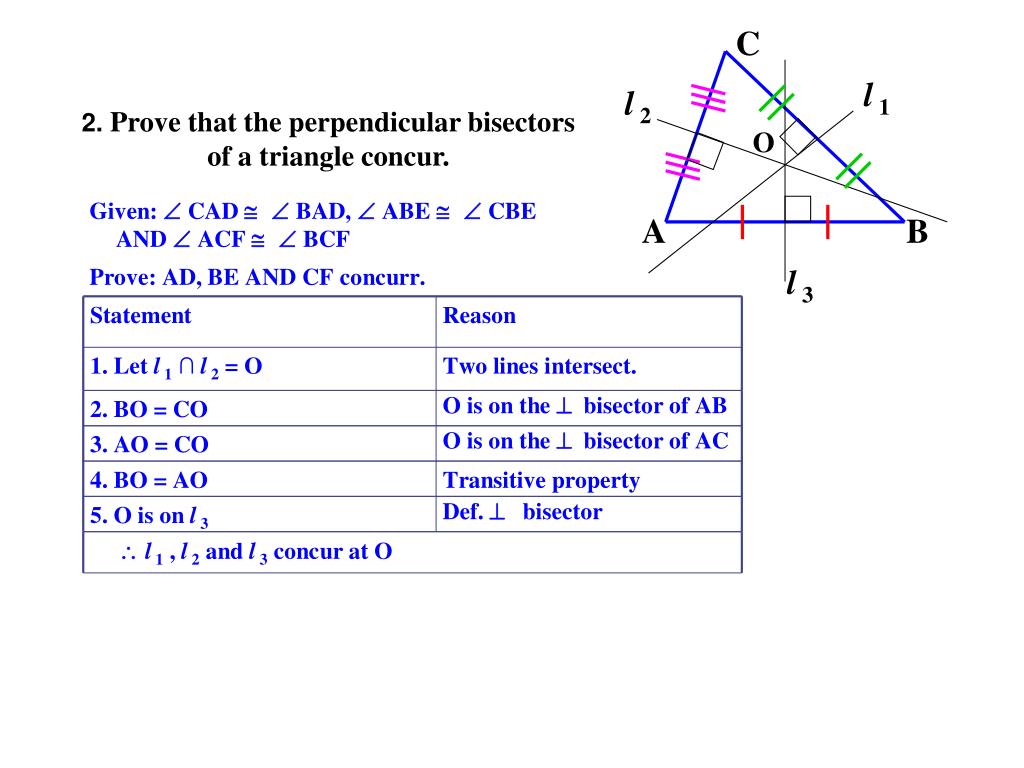

Level: High School, SAT Prep, GRE, GMAT, College. From this, we get that ∠BDA≅∠CDA as corresponding angles in congruent triangles. Recent Additions: Go Geometry theorems and problems involving circles and triangles, with animated proofs. Here, the additional given fact is that the line is an angle bisector, so ∠DAC ≅ ∠DAB, and from here it easily follows that ΔDAC is congruent to ΔDAB, using the Side-Angle-Side postulate. triangle show that bisector of angle formed between two similar sides is also a altitude, a median and a perpendicular bisector of side of that triangle. Altitude is the only term out of the three that do not start from a vertex. Their differences are that perpendicular bisector must be ninety degrees, or it'll be a median. Both median and altitude start from one of the three vertex. A segment that passes through the middle of the triangle. Writing an equation for medians, altitudes, perpendicular bisectors, and midsegments of a triangle. Passing through the midpoint is another similarity. 6 In ABC DE is perpendicular bisector of AC with D on AC. If AE 6 feet and BC 14 feet determine BE and CD. A segment with endpoints at the vertex and midpoint of the opposite side. We then take the given line – in this case, the apex angle bisector – as a common side, and use one additional property or given fact to show that the triangles formed by this line are congruent. Displaying top 8 worksheets found for - Answer Key Altitude Median. It is not difficult to prove, in the same manner, two symmetrical statements: - In an isosceles triangle the median drawn to the base. Since this is an isosceles triangle, by definition we have two equal sides.Īnd using the base angles theorem, we also have two congruent angles. we use congruent triangles to show that two parts are equal. In this proof, and in all similar problems related to the properties of an isosceles triangle, we employ the same basic strategy. not necessarily pass through C, which is indirect consequence of point that you made). Show that AD is perpendicular to BC: AD⊥BC Strategy Perpendicular bisector of AB is not perp from C to AB (i.e. This means the angle bisector is also the height to the base. Here, we will show the opposite: that the angle bisector is perpendicular to the base in an isosceles triangle. In another problem, we saw that in an isosceles triangle, the height to the base from the apex is also the angle bisector.


 0 kommentar(er)
0 kommentar(er)
